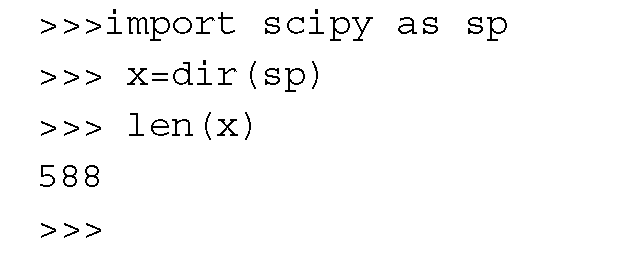В статье приведены несколько примеров, основанных на функциях, включенных в модуль SciPy. Функция sp.npv() оценивает текущую стоимость для заданного набора денежных потоков, при этом первый денежный поток происходит в нулевой момент времени. Первое входное значение - это ставка дисконтирования, а второе входное значение - массив всех денежных потоков.
Обратите внимание, что результат при ее использовании отличается от функции Excel npv().

Функция sp.pmt() используется для ответа на следующий вопрос.
Каков ежемесячный денежный поток для выплаты ипотечного кредита в размере 250 000 долларов в течение 30 лет с годовой процентной ставкой (APR) 4,5 процента, начисленной ежемесячно? Следующий код показывает ответ:
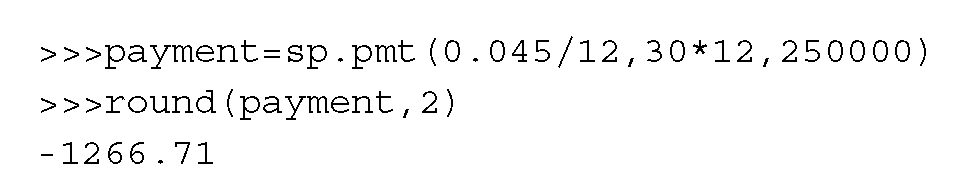
Исходя из предыдущего результата, ежемесячный платеж составит 1 266,71 доллара США. Может показаться странным, что у нас отрицательное значение. Фактически, эта функция sp.pmt() имитирует эквивалентную функцию в Excel, как мы увидим на следующем снимке экрана:
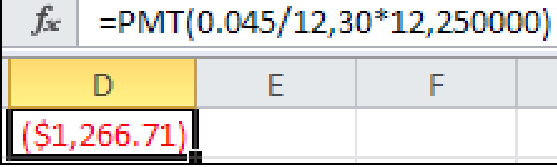
Входные значения: эффективная ставка периода, номер периода и текущая стоимость. Кстати, число в скобках означает отрицательное.
На данный момент просто игнорируйте отрицательный знак.
Точно так же функция sp.pv() копирует функцию Excel pv(). Для функции sp.pv() формат ввода:
sp.pv(rate, nper, pmt, fv = 0.0, when = 'end'),
где rate - ставка дисконтирования,
nper - количество периодов,
pmt - период платежа,
fv - будущее значение со значением по умолчанию, равным нулю.
Последняя входная переменная определяет, находятся ли денежные потоки в конце каждого периода времени или в начале каждого периода. По умолчанию это происходит в конце каждого периода. Следующие команды показывают, как вызвать эту функцию:
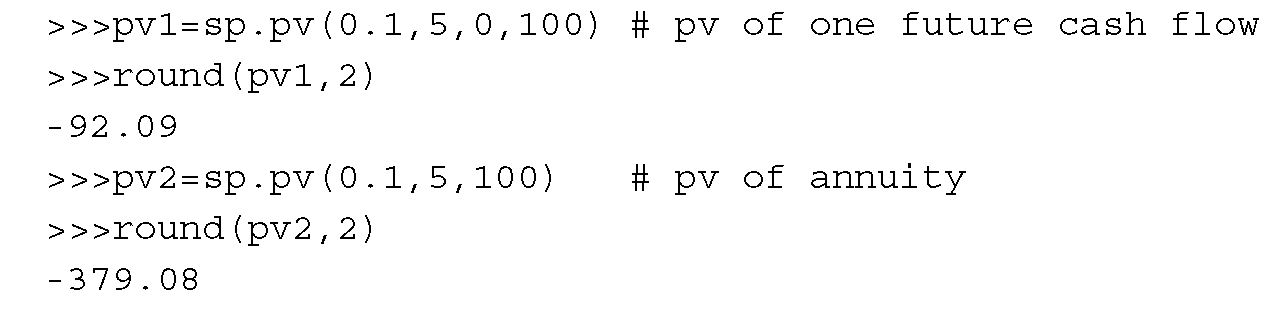
Функция sp.fv() имеет настройку, аналогичную настройке sp.pv(). В финансах мы оцениваем как средние арифметические, так и геометрические, которые определяются в следующих формулах.
Для n чисел x, то есть x1, x2, x3 и xn, мы имеем следующее:

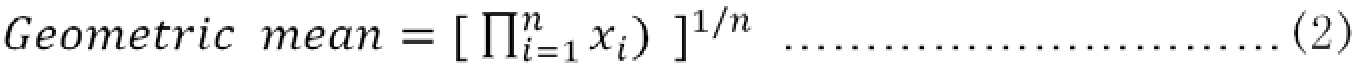
Здесь я» = 1 х т = X + х! 2 + ■■■ + х« и ПГ = 1 щ = (* я * ч * - ■ * х п ). Предположим , что мы имеем три числа а, Ь , и с. Тогда их среднее арифметическое является (а + B + C) / 3, в то время как их среднее геометрическое (а * Ь * с) л (1/3). Для трех значений 2 , 3 и 4, мы иметь следующие два средства:
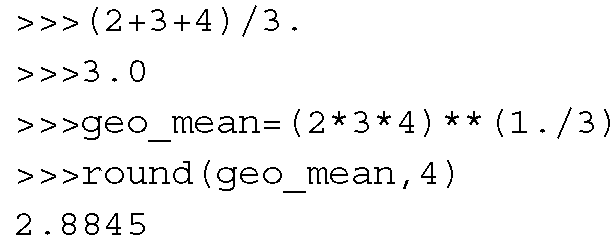
Если дано n результатов, формула для оценки их среднего арифметического остается прежней. Однако формула среднего геометрического дохода отличается, как показано здесь:
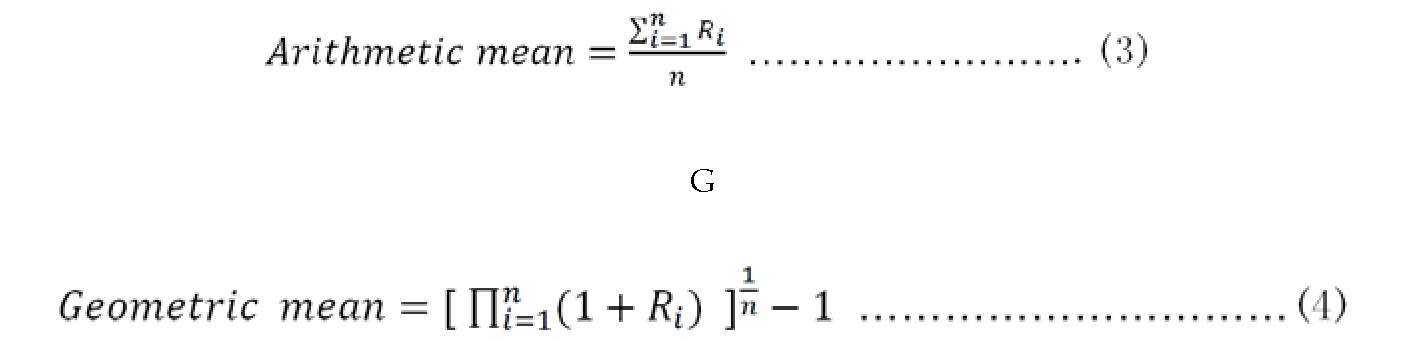
Чтобы оценить среднее геометрическое, будет применяться функция sp.prod(). Функция дает нам продукты всех элементов данных; см. следующий код:

Фактически, простая функция Python может быть написана всего с двумя строками для вычисления среднего геометрического для набора заданных результатов; см. следующий код:

Предыдущую функцию легко вызвать; см. следующий код:
Две другие полезные функции - это sp.unique() и sp.median(), как показано в следующем коде:
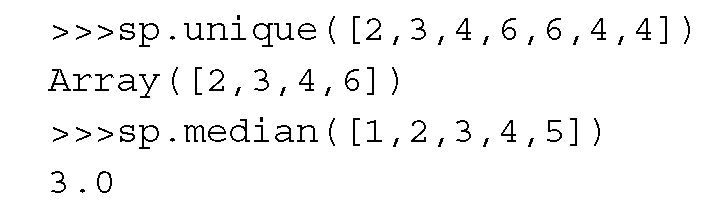
Функции Python sp.pv(), sp.fv() и sp.pmt() ведут себя как функции Excel pv(), fv() и pmt() соответственно. У них одно и то же соглашение о знаках: знак текущей стоимости противоположен будущей стоимости.
В следующем примере, чтобы оценить приведенную стоимость, если мы введем положительную будущую стоимость, мы получим отрицательную приведенную стоимость:

Есть несколько способов узнать все функции, содержащиеся в модуле SciPy.
Во-первых, мы можем прочитать соответствующие руководства. Во-вторых, мы можем выдать следующие строки кода:
Для экономии места в следующем коде показаны только несколько строк вывода: